Deep Neural Nets for Embedded Big Data Applications
We explore the use of deep neural networks (DNN) for embedded big data applications. Deep neural networks have been demonstrated to outperform state-of-the-art solutions for a variety of complex classification tasks, such as image recognition. The ability to train networks to both perform feature abstraction and classification provides a number of key benefits. One key benefit is that it reduces the burden of the developer to produce efficient, optimal feature engineering, which typically requires expert domain-knowledge and significant time. A second key benefit is that the network's complexity can be adjusted to achieve desired accuracy performance. Despite these benefits, DNNs have yet to be fully realized in an embedded setting. In this research, we explore novel architecture optimizations and develop optimal static mappings for neural networks onto highly parallel, highly granular hardware processors such as CPUs, many-cores, embedded GPUs, FPGAs, and ASIC.
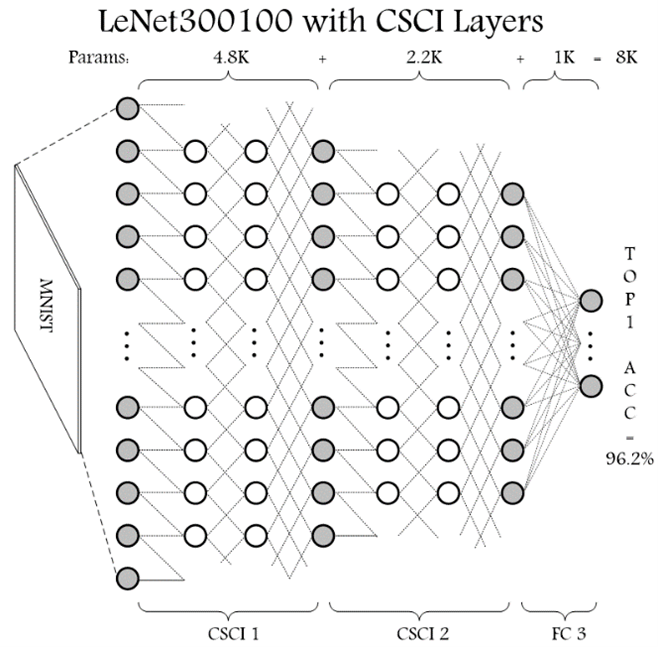
Two of the most popular optimization methods for DNNs include quantization and sparsification:
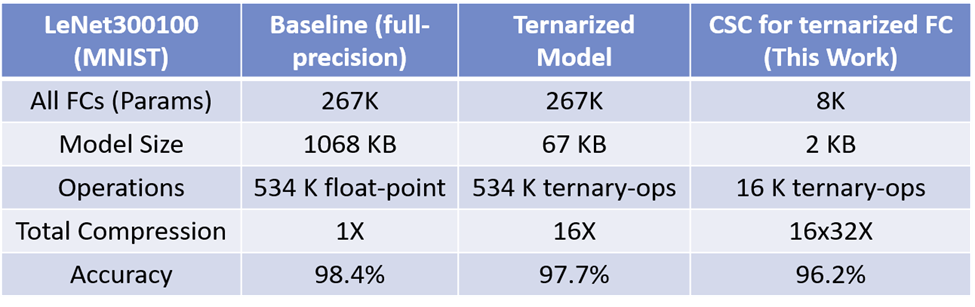
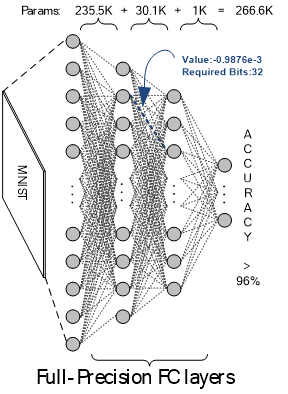
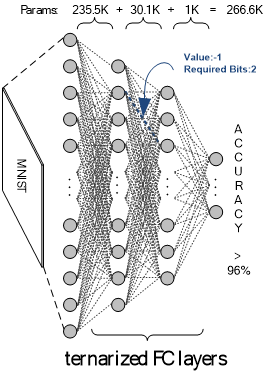
1) In quantization, the DNN model is trained such that the precision of parameters and the intermediate data, aka feature map, is lowered and limited to certain number of bits, and it can be applied on both weights and feature map of a DNN, e.g. 1 or 2 bits as in binary or ternary neural networks (BBNs and TNNs). With quantization, the model size shrinks proportional to the precision level, and the high-complexity operations (e.g. float-point multiplication) can be simplified with simple operations using simple hardware circuitry (e.g. XNOR logic as a multiplier for 1-bit values in BNNs).
2) In pruning methods, a DNN architecture in which zero values are omnipresent is pursued. Since the computation in DCNNs is dominated by multiply-accumulate (MAC) operations, everywhere that zero values exist the MAC operations can be skipped. This method is also referred to as fine-grained pruning, the main drawback of which is the irregular patterns of non-zero weights in the DNN model that necessitate having a compressing format and a decompression algorithm. Despite their efficacy, pruning methods are not suitable for extremely quantized DNNs.
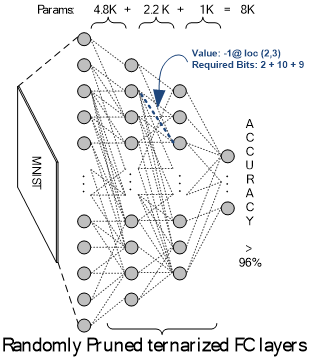
3) Structurally sparsifying DNN layers, on the other hand, are shown to be on par with pruning methods. Contrary to pruning methods that follow a train-prune routine, structurally sparsified methods can be considered as a prune-train routine in which the DNN is forced to be trained on an already-sparsified basis. The advantage of structural sparsity is two folds: exempting from indexing as required in pruning methods, and usability for extremely quantized DNNs.